Confusion Matrix, Accuracy, Recall, Precision, F1 score, Threshold , ROC Curve , AUC Score

정확도 (Accuracy)

아주 직관적이며 간단하다
$정확도 = {{정답과 일치한 수}\over{전체 데이터 수}} = {{TP + TN} \over {Total}} $
전체 범주를 모두 바르게 맞춘 경우를 전체 수로 나눈값이다.

정밀도 (Precision) : Positive로 예측한 것 중 올바른것

$정밀도 = {TP \over {TP+ FP} }$

재현율 (Recall) : 실제 Positive 중 올바르게 positive를 맞춘 것의 비율

$ 재현율 = {TP\over{TP+FN}}$

F1_score : 정밀도(Precision)와 재현율(Recall)의 조화평균

${F-점수} = { 2 \over { {1\over정밀도}+{1\over재현율}}} = {2*{Precision * Recall \over {Precision + Recall}}}$

Confusion Matrix

(Example)

from sklearn.metrics import plot_confusion_matrix

fig, ax = plt.subplots()
pcm = plot_confusion_matrix(grid_best_pipe, X_val, y_val,
                            cmap=plt.cm.Blues,
                            ax=ax);
plt.title(f'Confusion matrix, n = {len(y_val)}', fontsize=15)
plt.show()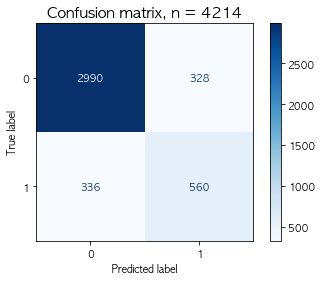

cm = pcm.confusion_matrix
correct_pred = np.diag(cm).sum()
total_pred = cm.sum()
print(f'[TP , TN] : {np.diag(cm)}') # TP + TN
print(f' TP + TN (정확하게 맞춘 예측) : {correct_pred}')
print(f' 총 예측 수 : {total_pred}')
print(f' 분류정확도 (Accuracy) : {round(correct_pred/total_pred,3)}')
print(f' Accuracy함수 accuracy_score : {round(grid_best_pipe.score(X_val,y_val),3)}')
print()     # 실제     기계
tp=cm[1][1] # 맞는걸   맞다해 
fn=cm[1][0] # 맞는데   틀렸데 
fp=cm[0][1] # 틀렸는데  맞았데 
tn=cm[0][0] # 틀린걸   틀렸다해 
print(f'정밀도 (Precision) : {tp/(tp+fp)}') # TP / TP + fP
print(f'재현률 (Recall) : {tp/(tp+fn)}') # TP / TP + fP

[TP , TN] : [2990  560]
 TP + TN (정확하게 맞춘 예측) : 3550
 총 예측 수 : 4214
 분류정확도 (Accuracy) : 0.842
 Accuracy함수 accuracy_score : 0.842

정밀도 (Precision) : 0.6306306306306306
재현률 (Recall) : 0.625

sklearn의 metrics의 모듈을 통해 혼동행렬을 만들어보았다.