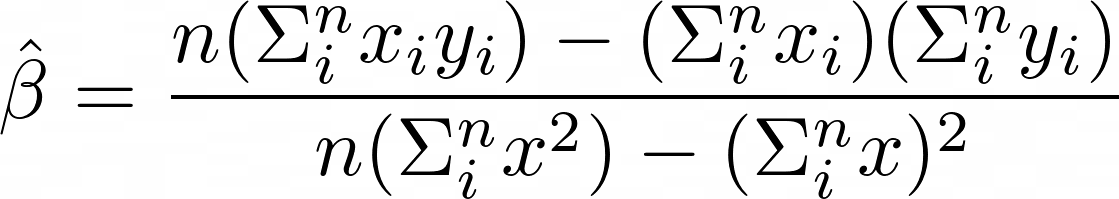Multiple Linear Regression 다중회귀
기존의 1 : 1 의 관계 ( $y = wx + b $)가 아닌 $y = w_1x_1+w_2x_2+w_3x_3 \cdots + w_nx_n + \beta$ 의 형태
Multicollinearity 다중공선성
다중회귀를 시작하면서부터는 변수선택의 문제가 발생하는데, (독립)변수들끼리 상관관계를 갖고있을 때 생기는 다중공선성을 염려해야함
독립변수들 간에 정확한 선형관계가 존재하는 완전공선성의 경우와 독립변수들 간에 높은 선형관계가 존재하는 다중공선성으로 구분하기도함
이는 회귀분석의 전제 가정을 위배하는 것이므로 적절한 회귀분석을 위해 해결해야 하는 문제가 됨.
진단법
결정게수 $R^2$값은 높아 회귀식의 설명력은 높지만, 식 안의 독립변수의 P-value 값이 커서 개별 인자들이 유의하지 않는 경우가 있다. 이런 경우 독립변수들 간에 높은 상관관계가 있다고 의심
독립변수들 간의 상관계수를 구한다.
분산팽창요인 (Variance Inflation Factor)를 구하여 이 값이 10을 넘는다면 보통 다중공선성의 문제가 있다
해결법
상관관계가 높은 독립변수 중 하나 혹은 일부를 제거.
변수를 변형시키거나 새로운 관측치를 이용
자료를 수집하는 현장의 상황을 보아 상관관계의 이유를 파악하여 해결
출처 : 위키백과
소거법
전진선택법 (Forward Selection)
참조:
https://todayisbetterthanyesterday.tistory.com/10
https://zephyrus1111.tistory.com/65
https://datascienceschool.net/03 machine learning/14.03 특징 선택.html
기존 모형에 가장 설명력이 좋은 변수를 하나씩 추가
유의수준을 통해 결정하는데, 이를 만족하지 못하면 선택되지 않음 → 전부 선택되지 않을수도있음!
$S$를 기존모형에 포함된 변수들의 집합, $\tilde S$를 모형에 포함되지 않은 변수집합 이라 하고 유의수준을 $\alpha$ 라 하자.
- 아직 모형에 적합시키지 않은 변수 ( $X_k \in \tilde S$ ) 를 기존 모형에 적합. (기존모형의 변수 + $X_k$ 를 통해 모형생성)

이때 최소 p-value 값과 유의수준을 비교하여 p-value < $\alpha$ 이면 최소 p-value에 해당하는 변수를 S에 포함, 1~2 단계 수행
# 참조 : https://zephyrus1111.tistory.com/65
## 전진 선택법
variables = df.columns[:-2].tolist() ## 설명 변수 리스트
y = df['Survival_Time'] ## 반응 변수
selected_variables = [] ## 선택된 변수들
sl_enter = 0.05
sv_per_step = [] ## 각 스텝별로 선택된 변수들
adjusted_r_squared = [] ## 각 스텝별 수정된 결정계수
steps = [] ## 스텝
step = 0
while len(variables) > 0:
remainder = list(set(variables) - set(selected_variables))
pval = pd.Series(index=remainder) ## 변수의 p-value
## 기존에 포함된 변수와 새로운 변수 하나씩 돌아가면서
## 선형 모형을 적합한다.
for col in remainder:
X = df[selected_variables+[col]]
X = sm.add_constant(X)
model = sm.OLS(y,X).fit()
pval[col] = model.pvalues[col]
min_pval = pval.min()
if min_pval < sl_enter: ## 최소 p-value 값이 기준 값보다 작으면 포함
selected_variables.append(pval.idxmin())
step += 1
steps.append(step)
adj_r_squared = sm.OLS(y,sm.add_constant(df[selected_variables])).fit().rsquared_adj
adjusted_r_squared.append(adj_r_squared)
sv_per_step.append(selected_variables.copy())
else:
break위와같은 식으로 전진선택법을 사용할 수 있으며, 그 외 후진선택법 등이 있다. 이는 코드블럭내의 블로그를 가면 자세히 설명되어있으니 그곳에서 읽어보는것이 더욱 도움될것이다.
sklearn.feature_selection.SelectKBest
사이킷런에서는 SelectKBest라는 모듈을제공하여, Feature Selection을 더욱 간편하게 해준다.
가장 성능이 좋은 변수만 선택해주며, K 라는 파라미터를 통하여, 몇개의 feature를 선택할 지 고를 수 있다.
from sklearn.feature_selection import f_regression, SelectKBest
## selctor 정의합니다.
selector = SelectKBest(score_func=f_regression, k=20)
## 학습데이터에 fit_transform
X_train_selected = selector.fit_transform(X_train, y_train)
## 테스트 데이터는 transform
X_test_selected = selector.transform(X_test)
all_names = X_train.columns
## selector.get_support()
selected_mask = selector.get_support() #이름만 가져온것
## 선택된 특성들
selected_names = all_names[selected_mask]
## 선택되지 않은 특성들
unselected_names = all_names[~selected_mask]
print('Selected names: ', selected_names)
print('Unselected names: ', unselected_names)그렇다면! k를 몇을 해야 가장 좋을까? -> 이전의 PCA나, 클러스터링에서 했듯 Elbow method처럼 plot을 그려보면된다!
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
training = []
testing = []
ks = range(1, len(X_train.columns)+1)
# 1 부터 특성 수 만큼 사용한 모델을 만들어서 MAE 값을 비교 합니다.
for k in range(1, len(X_train.columns)+ 1):
print(f'{k} features')
selector = SelectKBest(score_func=f_regression, k=k)
X_train_selected = selector.fit_transform(X_train, y_train)
X_test_selected = selector.transform(X_test)
all_names = X_train.columns
selected_mask = selector.get_support()
selected_names = all_names[selected_mask]
print('Selected names: ', selected_names)
model = LinearRegression()
model.fit(X_train_selected, y_train)
y_pred = model.predict(X_train_selected)
mae = mean_absolute_error(y_train, y_pred)
training.append(mae)
y_pred = model.predict(X_test_selected)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
testing.append(mae)
print(f'Test MAE: ${mae:,.0f}')
print(f'Test R2: {r2} \n')
plt.plot(ks, training, label='Training Score', color='b')
plt.plot(ks, testing, label='Testing Score', color='g')
plt.ylabel("MAE ($)")
plt.xlabel("Number of Features")
plt.title('Validation Curve')
plt.legend()
plt.show()
참 편하게도, 이렇게 feature의 변화가 K-best로 뽑혔을 때 MAE 가 낮아지는 정도를 볼 수 있으니 참 좋다!
## 실습
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score
from sklearn.preprocessing import StandardScaler, RobustScaler
features , test = ['sqft_living', 'sqft_lot'], ['price']
x_train = df_train[features]
y_train = df_train[test]
x_test = df_test[features]
y_test = df_test[test]
x=dfraw.loc[:,features].values
x=StandardScaler().fit_transform(x)
x_train_Standard=pd.DataFrame(x, columns=[features])
y=dfraw.loc[:,test].values
y=StandardScaler().fit_transform(y)
y_train_Standard=pd.DataFrame(y, columns=[test])
# Train의 경우 model을 학습시키고, model을 뱉어낸다.
# Test의 경우, 입력된 모델의 predict만을 이용하여 시행하고, 결과를 뱉어낸다
def regression_test(model,xtrain, ytrain , isTrain='test'):
try:
if isTrain.upper()=='TRAIN': #Training부터 시작하는 경우 (트레이닝)
print('Start with Training')
model = LinearRegression()
model.fit(xtrain,ytrain)
except:
pass
y_pred = model.predict(xtrain)
mse = mean_squared_error(ytrain, y_pred)
mae = mean_absolute_error(ytrain, y_pred)
rmse = mse ** 0.5
r2 = r2_score(ytrain, y_pred)
dic={'mse':round(mse,2),'mae':round(mae,2),'rmse':round(rmse,2),'r2':round(r2,2)}
# print(f'MAE : {dic[mse]}\nMAE : {dic[mae]}\nRMSE : {dic[rmse]}\nR_Square : {dic[r2]} ')
return model,dic
model_st_3, std_dic=regression_test(model, xtrain=x_train_Standard, ytrain=y_train_Standard, isTrain='train')
std_dic
# Start with Training
# {'mae': 0.47, 'mse': 0.51, 'r2': 0.49, 'rmse': 0.71}
regression_test(model_st_3, x_test,y_test) # StandardScaler
#(LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False),
# {'mae': 541048.28, 'mse': 424174008111.0, 'r2': -2.22, 'rmse': 651286.43})'Machine Learning > Linear Models' 카테고리의 다른 글
| Simple Linear Regression ( 단순 선형 회귀 ) (0) | 2021.02.07 |
|---|