eyebrow93

출처 :
XGBoost: A Scalable Tree Boosting System / Tianqi Chen , University of Washington
www.youtube.com/watch?v=ZVFeW798-2I&list=RDCMUCtYLUTtgS3k1Fg4y5tAhLbw&start_radio=1&t=900 

Ensemble 모델 중 Boosting의 Gradient 부스팅의 상위호환버전과도 같은 XGBOOST이다. 

강력한 성능을 가진 XGBoost의 논문과, StatQuest의 강의를 열심히 공부하여 아래와 같이 정리해본다. 

초기 prediction 을 만들고 (default=0.5) 시작하는 것은 기존의 부스팅과 동일하다. 그러고 나서 잔차를 먼저 하나의 리프에 넣어준다. 

그리고, 해당 leaf의 Similarity Score를 계산하는데,

$$ {Similarity.Score} = { Sum. of. Residuals, Squared \over{Number. of. Residuals + \lambda }} = { (\Sigma_{i=1}^{n}{Residual})^2 \over { n +\lambda}  }$$
n=해당 leaf의 Residual 수

여기서 $\lambda$는 Regularization Parameter로 우리가 지정해주는 것이다. 
StatQuest에서는 간단하게 설명하기위해 4개의 row를 가진 데이터를 예를 들었다.

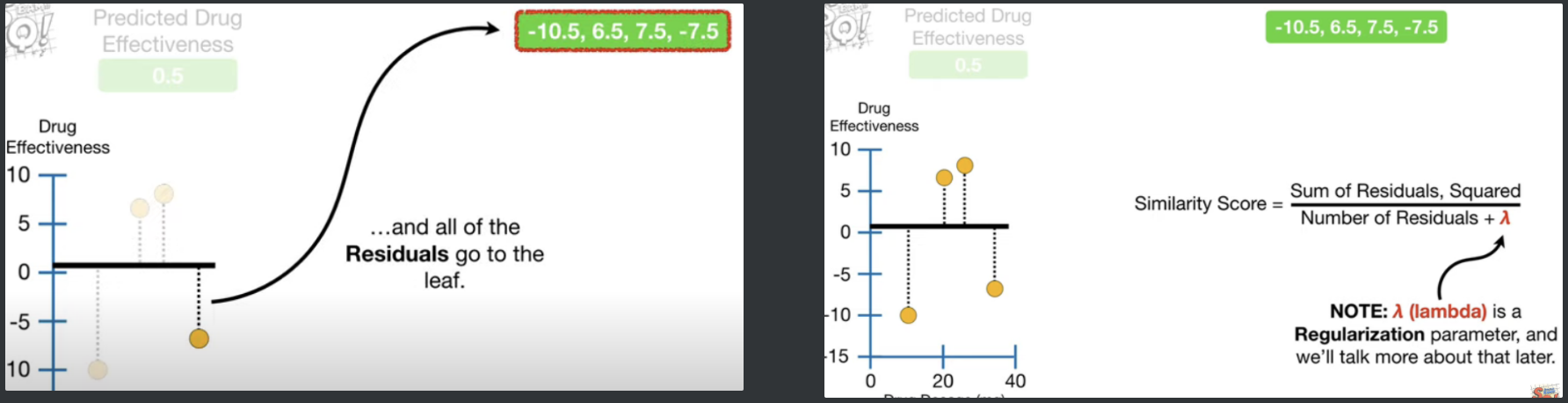
최 상위 4개가 들어있을때의 SS는 $(-10.5+6.5+7.5-7.5)\over{4 + \lambda}$이고, 람다를 0이라 가정했을때 (계산을 간편히하기위해)
SS=4이다. 

SS(Similarity Score) 계산이 끝나면 이제 이 리프를 분기시켜서 트리를 만들어본다.
4개의 데이터 사이에 분기점을 만들면 총 3개를 만들 수 있고, 이렇게 분기되는 때마다 SS를 계산하여, Gain을 계산한다.
각 트리를 만들때마다 왼쪽, 오른쪽 리프의 SS계산을 하여 기록하면 이제 분기 전후에 대한 비교가 가능해진다. 
분기 전에는 7.5와 -7.5가 서로 상쇄시켜서 ss가 낮았던 반면, 분기 후엔, 왼쪽 오른쪽 리프들 각각 상쇄작용이 약해서 ss점수가 더 크다. 

이제 각 분기점에 대한 Gain을 계산하는데, Gain의 식은 이러하다. $$Gain = Left_{Similarity} + Right_{Similarity} - ROOT_{Similarity}$$

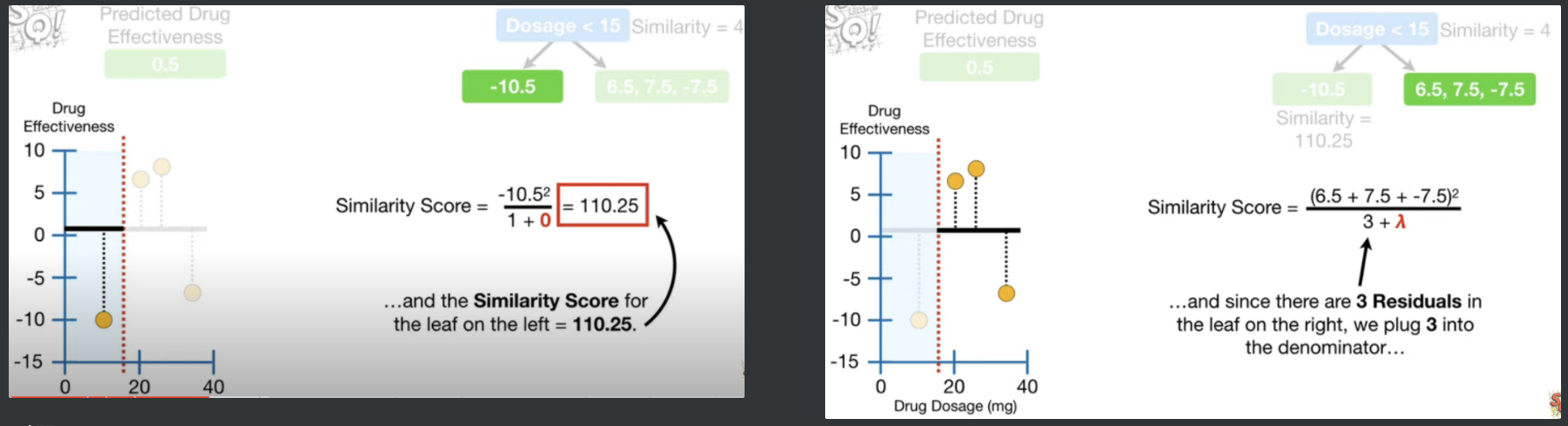
분기점을 1번과 2번데이터 사이(Dosage < 15)로 했을때 Gain은 120.33이다.

22.5를 기준으로 분기하면 왼쪽에 잔차는 -10.5 , 6.5 이고, 오른쪽 잔차는 7.5 , -7.5로

$\lambda=0$으로 설정하였으니 각각의 SS는 $왼쪽 = {{(-10.5 + 6.5)}^2 \over {2 + \lambda}}= {4^2 \over {2}} = 8$ , $오른쪽 = {({7.5-7.5})^2 \over{2+\lambda}}=0$에서 왼쪽이 8 오른쪽이 0이고, Gain은 $8+0 -4 = 4$ 이다.

이제 분기점을 3,4번 데이터 사이 (Dosage < 30)으로 했을 때를 계산하면 

더이상 관측치 사이에 Split 할 것이 없다. 따라서 각 분기점의 Gain을 비교하면, 1,2번 사이의 Gain (120.33)이 가장 크므로, Dosage < 15을 선택.
왼쪽 리프에는 -10.5 하나만 들어와있고, 오른쪽엔 6.5, 7.5, -7.5가 들어와있다. 

이제 오른쪽 리프에 3개를 분할해보는데, 맨 처음 루트에서 SS와 각각 split지점에 대한 SS, Gain을 계산했던 것과 동일하게 진행한다.
2,3번 사이에 split을 하면, 아래 그림과 같이 나눠지고

그때의 SS와 Gain은 
$SS_{(Dosage<22.5)} = {  {(6.5+7.5-7.5)^2}\over{3+0} } = 14.08  $, $SS_{left}= {{(6.5)^2}\over{1+0} }= 42.25$ , $SS_{right}= { { (7.5-7.5)^2 } \over {2+0} } = 0$이고,
${Gain} = { SS_{left} + SS_{right} - SS_{ROOT} } = {42.25 +0 - 14.08} = 28.17$ 이다.

이후, 

3,4번 사이에 split을 하면, 아래 그림과 같은 분기가 이루어지고, 이 떄의 SS를 계산하면 각각 
$SS_{(Dosage<30)} = {  {(6.5+7.5-7.5)^2}\over{3+0} } = 14.08  $ ,  $SS_{left}= {{(6.5+7.5)^2}\over{2+0} }= 98$ , $SS_{right}= { { (-7.5)^2 } \over {2+0} } = 56.25$이고, 
${Gain} = { SS_{left} + SS_{right} - SS_{ROOT} } = {98 + 56.25 - 14.08} = 140.17$ 이다. 

22.5로 나눴을 때 보다, 30으로 나눴을 때 더욱 Gain이 크므로, Dosage < 30 을 선택한다. 
이후, max_depth (default = 6) 이 허용하는 만큼 한번 더 왼쪽 리프를 분기할 수 있지만, 계산을 간편히 하기위해 max_depth = 2로 제한하여 분기종료. 

이로써, SS Score와 Gain 을 통하여 트리를 만들었다. 
이제 트리를 Prune해야한다. Prune에서는 Gamma($\gamma$)를 사용한다. 
Gain보다 $\gamma$가 크면 가지친것을 삭제하는 것이다.

$\gamma = 130$이라면, 오른쪽 분기점의 Gain ( 140.17 )이 더 크므로 오른쪽 brunch가 살아남는다, 이에따라, 루트도 함께 살아남게된다.

만약 $\gamma=150$이라면?

먼저 오른쪽 brunch의 gain이 150보다 작으므로, 삭제하고, 루트또한 gain이 120.33으로 150보다 작으므로 이번에 만든 트리 자체를 날려버리는 것이다. 

$\lambda$의 역할은?

람다가 어떤 정규화 파라미터로 작용한다는 것은 앞서 설명했다. 하지만 어떻게 작용하길래 정규화 파라미터역할을 하는 것일까?
이는 Similarity Score를 확인하면 알 수 있다.

$$ {Similarity Score} = { { { Sum.Of.Residuals  }^2} \over {Num.Of.Residuals + \lambda }  }$$

$${Gain} = { SS_{left} + SS_{right} - SS_{ROOT} } $$

에서, $\lambda$가 커질수록, SS는 작아지고, 이에따라 Gain도 같이 작아지게된다. XGBoost에서 Gain에 따라 Pruning을 진행하는데, $\gamma$값보다 Gain이 작으면, 그 트리(or Brunch)를 삭제하므로, 트리가 자주 지워지게되고, 이는 결국 Overfitting을 방지하는 역할을 하게된다!

λ 값에 따른 Gain의 차이가 위와같다. SS를 계산할 때,  λ가 분모에 들어있으므로,  λ가 커지면 -> SS가 작아지고, 이에따라 Gain도 작아지는 것이다.

하나의 리프 내 샘플의 수에 따라서 λ가 어떤 영향을 주는가? 

SS와 Gain 모두 Number of Residual로, 한 리프에 몇개의 샘플(잔차)이 들어있는지에 영향을 받는다.
λ는 모두 분모에 있으며, 이에 대한 영향은 λ가 1만큼 커짐에 따라, Residual이 1개있는 리프는 SS가 $1\over2$만큼 작아진다.
2개있을경우 분모가 2->3으로 변화하므로 한 leaf에 잔차 수가 많으면 많을 수록 λ의 영향이 작다는것이고, 이는 한 leaf의 샘플 수가 많을 수록 λ의 영향이 적어지므로, 향후 파라미터 튜닝에서 λ의 값과, min_samples_leaf를 함께 생각해야 할 것이며 이 둘의 상호 영향또한 염려해야한다는 것으로 이해된다.

위의 내용에 대한 정리

$$ {Similarity.Score} = { Sum. of. Residuals, Squared \over{Number. of. Residuals + \lambda }} = { (\Sigma_{i=1}^{n}{Residual})^2 \over { n +\lambda}  }$$
$${Gain} = { SS_{left} + SS_{right} - SS_{ROOT} } $$
n=해당 leaf의 Residual 수
λ가 0보다 커진다 = Gain이 작아진다 = Leaves를 Prune하기 쉬워진다 = OverFitting을 방지한다 
$\gamma$가 커진다 = Gain-$\gamma$가 음수가 될 확률이 높아진다 =  Brunch를 Prune하기 쉬워진다 = OverFitting을 방지한다.